Forget the rule of thirds. My new favourite compositional device is the golden ratio. But what does a formula described by a 13th century Italian mathematician have to do with taking pictures? And what on earth does a recursive spiral have to do with street photography? It’s all about the intersection of mathematics, history, and art. Read on to dive deeper into the mystery.
Somewhere along the line, I learned about the ‘rule of thirds’, a helpful approach to composing better photographs. I adopted the technique enthusiastically. Placing the subject one third of the way across the image, rather than in the centre, was soon my default approach. So, I always have a three-by-three grid switched on in the electronic viewfinder of my Q- and SL-series Leica cameras. It is one of several available ‘capture assistants’, and great for either centring objects in the frame, or placing them on the ‘one-third’ line.
Mathematical magic from the Middle Ages
But, as I learned more about photographic composition, I realized there were other nifty strategies available to me. In particular, I learned of one whose origins appeared to lie at least as far back as the Middle Ages. I found its connection to both mathematics and art fascinating.


This compositional ‘rule’ goes by numerous names, such as: the golden ratio; the golden rectangle; or the Fibonacci spiral. All three terms convey a flavour of their geometric roots, but they are not mathematically identical. I hope to clarify the relationship between them, while illustrating how they have infiltrated my street photography.
Let’s start with the Fibonacci spiral, based upon the Fibonacci sequence, and named after an Italian mathematician born in 1170. It is likely that his famous number sequence was already known from earlier work by Indian mathematicians. But Fibonacci brought it to the attention of western science. Here it is:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
The underlying formula is elementary: each new number in the progression is the sum of the previous two numbers. So, 3 follows from 1 + 2, just as 5 follows from 2 + 3. The numbers in the sequence are referred to as Fibonacci numbers. They are famous because they are observed unexpectedly in many natural phenomena. Examples include branching of trees, fruit sprouts on pineapples, and the flowering of an artichoke.


Spiralling out of control
Fibonacci numbers give rise to a spiral, as illustrated in the diagram below. Squares with the dimensions of each Fibonacci number can be packed together perfectly in sequence. This is not magic, but the result of each number in the sequence being the sum of the previous two numbers. So, the length of the side of each larger square is the sum of the lengths of the sides of the two previous squares. Get it?
The size of the ensemble grows as a new square is added for each new number in the sequence.

When a quarter-circle curve is drawn corner-to-corner across each square, the resulting continuous line forms an ever-increasing spiral. You can see it in blue in the diagram; this is the Fibonacci spiral.
Leica meets Fibonacci
Have a look at the overall shape of the ensemble of squares in the diagram. Does it remind you of anything? What about a camera viewfinder, or a frame in a 35mm film, or a full-frame sensor?
The ratio of long side to short side in the diagram is (21+13) to (13+8), or 34 to 21. That corresponds to a ratio of 1.619. If you were to calculate that ratio for larger and larger ensembles of squares, it would gradually approach 1.618. We could add many more decimal places if we wanted to. That number is called the golden ratio.
I will come back to this shortly.


As we know, the dimensions of a 35mm frame are 36mm on the long side and 24mm on the short side. That’s not so far from 34 and 21. This is why the shape of the rectangle in the diagram resembles that of a 35mm frame.
The story of why the designers of the first compact still cameras, including Leica, chose that 24 x 36 mm frame size is a fascinating one. They repurposed the readily available 35mm movie film stock, running it horizontally through the camera rather than vertically. This allowed them to align eight sprocket holes on the film to each exposed image, rather than the four sprocket holes per frame used when running vertically. As a result, they could switch the format from 4:3 to 3:2, or 36mm x 24mm. This has since become the standard for full-frame film and digital photography. In a remarkable coincidence, it resembles a shape resulting directly from a mathematical formula described in the 12th century.
What does this mean for those of us composing photographs?
The golden ratio in art
The golden ratio is usually written as the Greek letter phi (φ), and, like its cousin pi (π), is an irrational number. Although known to the Ancient Greeks, it became linked with art in the early 16th century. The Italian mathematician Luca Pacioli published a book titled De divia proportione, attributing to the ratio an orderliness and simplicity that must have been divinely ordained. The book featured illustrations by none other than Leonardo da Vinci.
Over the following centuries, the golden ratio has assumed an almost mystical reputation. Enthusiasts have equated it with a mathematical distillation of beauty. It is said that artworks incorporating dimensions reflecting this ratio are pleasing to the eye.


I have found no clear evidence that the work of the great Renaissance masters built upon the golden ratio. But, apparently, many enthusiasts believe this is the case.
So, just as the golden ratio imbues some aesthetic oomph to paintings, should it not do the same for photographs? Along with the rule-of-three, and leading lines, it has indeed become a staple of compositional instruction. So, how does a photographer make use of it?
Throughout the article, I have provided examples of how I have used it. In each case, you can see the image I shot. The parallel image, a screenshot from Lightroom, shows how the golden ratio, in the form of a Fibonacci spiral, is superimposed. I have taken advantage of that resemblance between the photo-frame and the shape of the Fibonacci spiral diagram.


You should be able to spot how the human form in each photograph is located at the centre of the spiral. Before discussing the artistic merits of this approach, though, let’s first clear up a mathematical point.
Golden spirals versus Fibonacci spirals
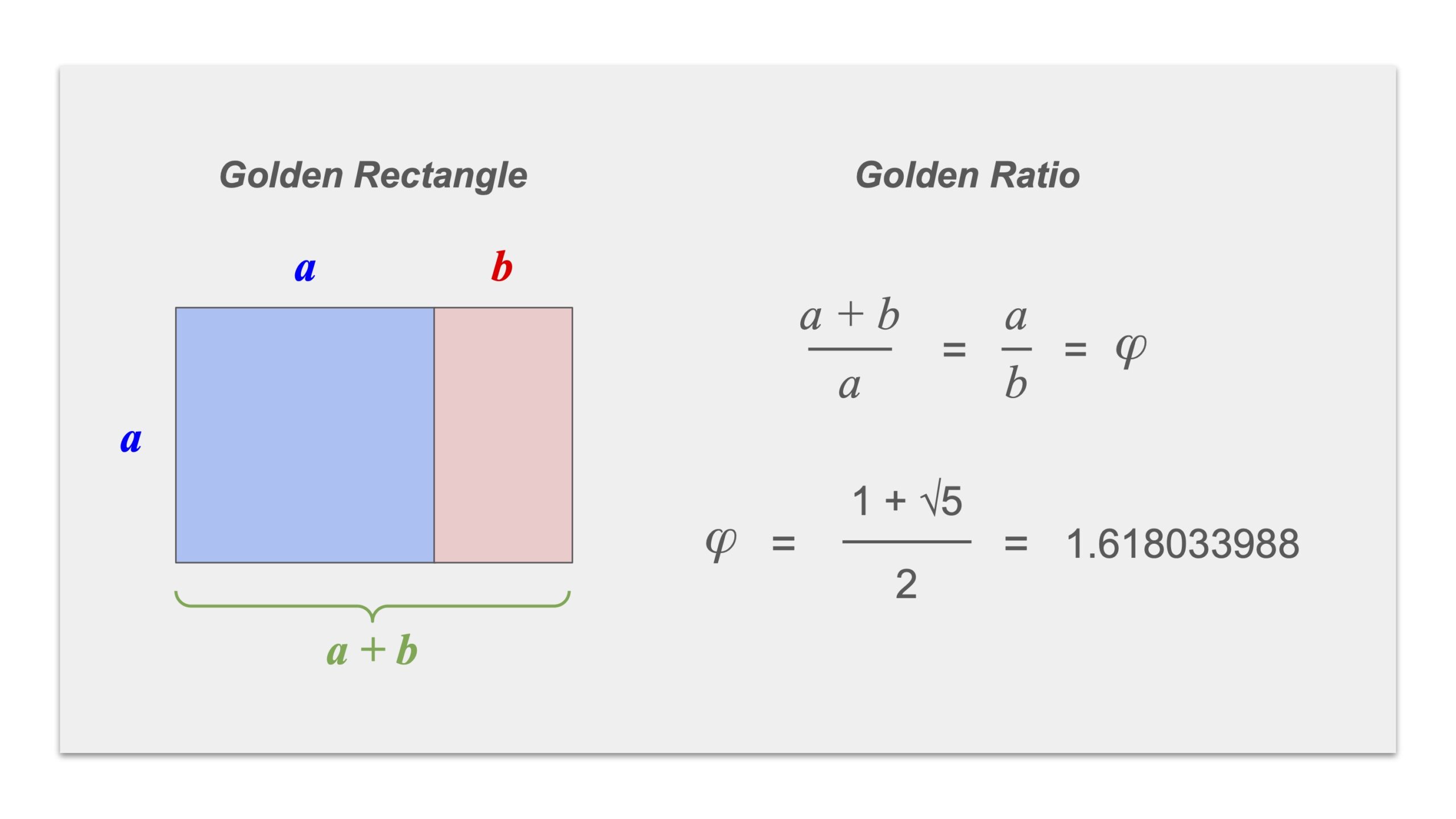
I mentioned earlier that as a Fibonacci spiral grows in size, its behaviour approaches more closely the golden ratio 𝜑 (~1.618). However, there is a more direct way to produce a spiral based upon the golden ratio. This is accomplished using a golden rectangle.
The golden rectangle is unique in that it has a long side, (a + b), and a short side (a), such that the ratio of (a + b) to (a) is the same as the ratio of (a) to (b). That ratio is 𝜑. This is illustrated in the diagram below.
If you write this relationship as an equation, you can calculate the value of 𝜑.
You can go on to create a golden spiral using the approach applied earlier to the Fibonacci numbers. That is, packing golden rectangles together and drawing quarter-to-quarter curves within each a-by-a square. Unlike the Fibonacci spiral, whose dimensions steadily approach the golden ratio as it grows, this spiral reflects perfectly the golden ratio at all sizes.

A pot of gold at the end of the rainbow spiral
Have you had enough gold yet? Between the golden ratio, golden rectangles and a golden spiral, there’s plenty to go around. The question is, have these concepts aided my photographic compositions?


As we all know, whether a photograph or a painting is aesthetically pleasing is a matter of personal taste. Determining if the elements in an image are well-balanced and optimally arranged is not a quantitative science. What I can say, however, is that I have found the Fibonacci spiral very useful. In particular, in deciding how to arrange images in which a human form competes with the other elements calling for attention.
Street photographs inevitably include background information, which can either add to or detract from the success of the image. In fact, that background context almost defines street photography. I think the Fibonacci spiral represents a useful strategy for managing the potential background distractions present in street photographs.
How do I use the Fibonacci spiral in practice?
I can assure you that I do not have the spiral drawn on the rear screen of my camera, or displayed in its EVF. Having become familiar with the concept, I do though think about it when framing a shot. I also leave myself room when composing to make post-processing adjustments in the position of the subject.


Lightroom is very helpful here. Its ‘crop’ feature has a number of useful compositional aids. The default option is the three-by-three grid, of which I am very fond. However, if you press the ‘O’ key whilst hovering over the selected region of an image, you can choose other options. The golden spiral is one of these.
Furthermore, the spiral can be superimposed on an image in multiple ways. Simultaneously pressing ‘Shift’ and ‘O’ allows you to cycle through the various permutations.
Using these two features, I can experiment with alternative arrangements of subject and context, with an eye on how they relate to the spiral.
I wonder if Leica will ever offer a Fibonacci spiral as an option among its capture assistants. I would definitely use it! Perhaps other camera manufacturers already do this? Please let me know in the comments if you have further information about this.


The Fibonacci spiral — a thing of beauty
Whether you are mathematically minded or not, I hope you find the creation of beautiful spirals from either Fibonacci numbers or the golden ratio, satisfying at some level. It might be hard in modern times to embrace the view that mathematical constructs play a mystical role in art. On the other hand, the ability of art itself to evoke an emotional response in humans remains mysterious.
Perhaps there is some feature of our brains, not yet understood, which connects art and mathematics at a subconscious level. Whatever the explanation, I suspect the golden ratio will continue to intrigue artists who seek a harmonious balance in their creations.


Have you used the golden ratio or the Fibonacci spiral in your photography? Do you use capture assistants to aid your composition? Which of the Lightroom capture assistants is your favourite? Please let us know in the comments below.
Join the Macfilos subscriber mailing list
Our thrice-a-week email service has been polished up and improved. Why not subscribe, using the button below to add yourself to the mailing list? You will never miss a Macfilos post again. Emails are sent on Mondays, Wednesdays, and Fridays at 8 pm GMT. Macfilos is a non-commercial site and your address will be used only for communications from the editorial team. We will never sell or allow third parties to use the list. Furthermore, you can unsubscribe at any time simply by clicking a button on any email.

Does anyone know if there is such a function in dxo Photolab?
Thank you for a fascinating article that explains and compares three compositional aides in vusual art.
BTW. the mathematical ‘rules and regulations’ used in music are imminent, so why wouldn’t they be in the visual arts?
Sorry for the typos
Thanks Gerard. Glad you enjoyed the article. Thanks for highlighting the importance of mathematical frameworks in music, and the parallel with the visual arts. All the best, Keith
I didn’t realize this feature was hidden in Lr, thanks for the enlightenment! I have been playing around with it for the last half an hour. 🙂
Not a Leica feature, but apparently Sony (for a fee, of course) will bake any crop overlay you want into your Sony camera body. The Fibonacci Spiral was listed as one of the options. How crazy is that?
Hi Brandon, thanks for the information about the Sony Fibonacci Spiral option. That is wild. I wonder what it would take to convince Leica to offer it in a future software upgrade. Because it does not sit symmetrically in the frame, it would have to be available in four configurations, so there would also need to be a way to toggle between them. Complicated! All the best, Keith
Fascinating article. And I find the compositions you chose very pleasing to my eye. I have been aware of the Rule of Thirds and Golden Ratio, but not the Fibonacci spiral. I tend to compose intuitively, with these guidelines (so to speak) in the back of my mind. I do think my compositional skills have grown over the years because of awareness of guidelines.
In an aside, when Nippon Kogaku (Nikon) first produced a 35mm camera, in 1948, they chose a 32mm X 24mm format. This was a mindful choice, for two reasons. First, the format was a compromise between 3-1/2 X 5, 5 X7, and 8 X 10 paper formats, the most popular print sizes, so less “waste” of image. Second, it yielded 40 images per roll, instead of 36, which presumably Nikon thought would be a competitive advantage. Alas, Japan was under American occupation at the time, and the Powers That Be did not like that the 36mm X 24mm was not compatible with standard 35mm in the U.S. So by 1951, to promote exports to USA, with the Nikon S, they had switched to 36mm X 24mm.
I found through most of my photographic “career”, I wished Nikon had stuck with 32mm X 24mm! It was only when 35mm became popular with snapshooters that 4 X 6 and 8 X 12 prints became readily available.
Hi Martin, I’m glad to hear that you enjoyed the article. Although some people balk at the notion of ‘rules’ or ‘guidelines’, in general, I think it is helpful to have tried and tested frameworks to call upon, particularly for beginners. This probably applies in many walks of life. Thanks also for the additional information about the Nikon 32mm x 24mm format. I rarely crop to 4×3. More likely, it would be 5×7, especially for images in portrait format, so that they are suitable for Instagram posts! All the best, Keith
Thanks for taking us to somewhere we’ve never thought of visiting. Never gave it a thought, but your arguments make sense (now I think of it). Great photos too.
Hi Andy, many thanks! Glad you found it is interest. All the best, Keith